Imagine you had time travelled back to antiquity and, without a ruler or special tools, needed to produce a straight line. This might be the basis for a lathe bed, axle turning machine, rifle boring device or a host of other requirements.
How would you do it?
One obvious way is to simply stretch a taut string between two points, and run a marker along it. But owing to the flex in the cord, that is not going to be rigid enough for accurately moving a toolbit or graver to cut metal.
Can a basic machine be cobbled together to produce something with a reasonable degree of accuracy?
It turns out, you can, if you are able to gather together two or more long pieces of, say, timber (and they don’t even need to be straight) and be able to bore holes through the ends at the same time. Then afterwards, fix well-fitting axles (say round cross-section branches) through these to act as pivots and as such a great deal of the problem is solved.
So much so that in 1877 AB Kempe wrote a treatise titled ‘How to draw a straight line: a lecture on linkages‘ detailing, as the name implies, producing straight lines from linkages.
In it he details a variety of mechanisms. I was able to recreate some of these with LEGO Technic and a pen so here they are. Note the pen is a bit jittery as I should have placed a smooth surface (eg. LEGO flat tiles) under the drawing area.
Watt’s mechanism
This three bar linkage is attributed to the great engineer James Watt, and is figure 2 from Kempe’s book. The marker (a pen refill in this case) is placed in the middle of the centre beam and traversed vertically. For a measure it travels straight, but if taken too far then deviates in an arc. If pushed at both limits the appearance is very much like an integral sign.
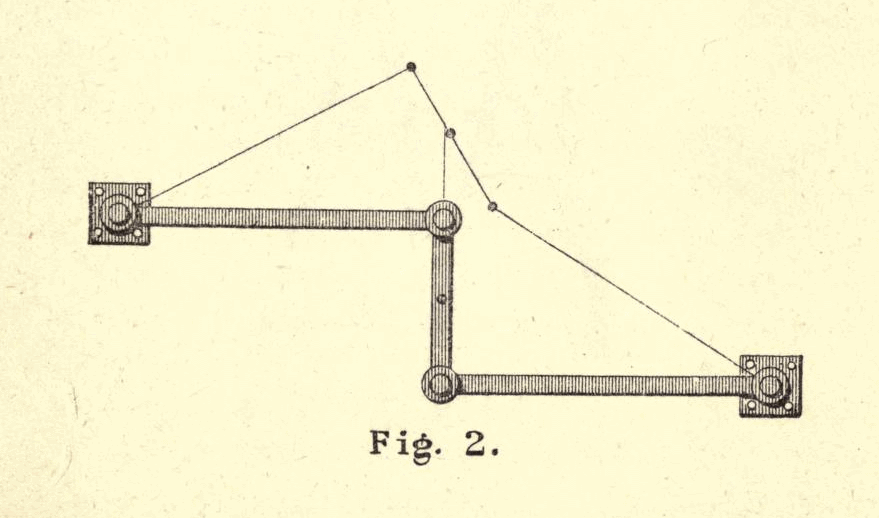 |
|
Richard Roberts mechanism
Figure 3 from Kempe. The marker or engraver is placed in the bottom point of the moving Isosceles triangular arm and traversed horizontally. All beams are the same length except the top one is about half the length.
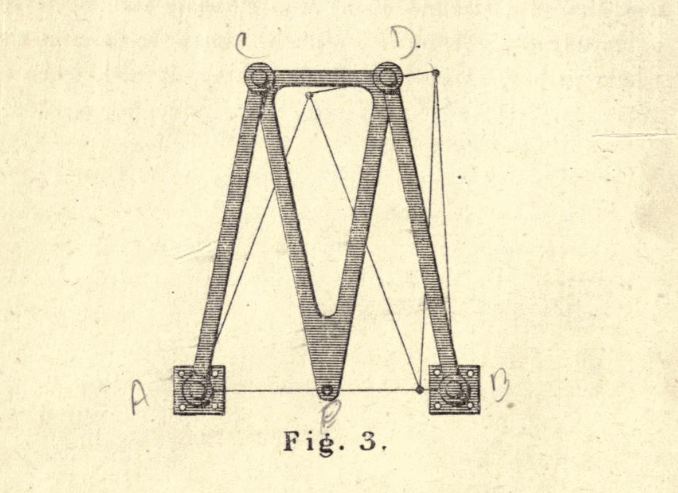 |
|
Peaucellier’s mechanism
Figure 5 from Kempe. The use of a kite arrangement allows the production of a longer line than Watt’s mechanism.
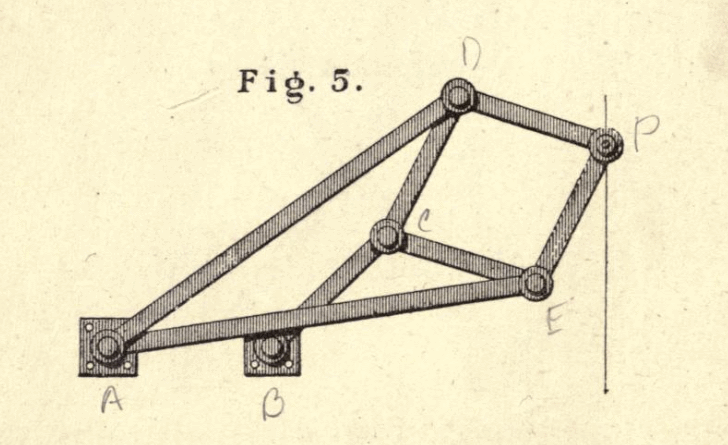 |
|
A-frame mechanism
I forgot where this one came from, it’s not in the treatise.
| I can’t find a pic of this one |
|
Conclusion
There are a number of other mechanisms in Kempe’s book so perhaps sometime I may also try them out in LEGO.